深度学习在序列化推荐中的应用(2)
前言
基于上一篇GRU4REC的继续聊聊深度学习在推荐系统中的应用
NARM
作者提出了一种混合Encoder的方式:全局(Global)所有的序列信息的Encoder和当前(Local)Session序列的Encoder
所以他的模型是: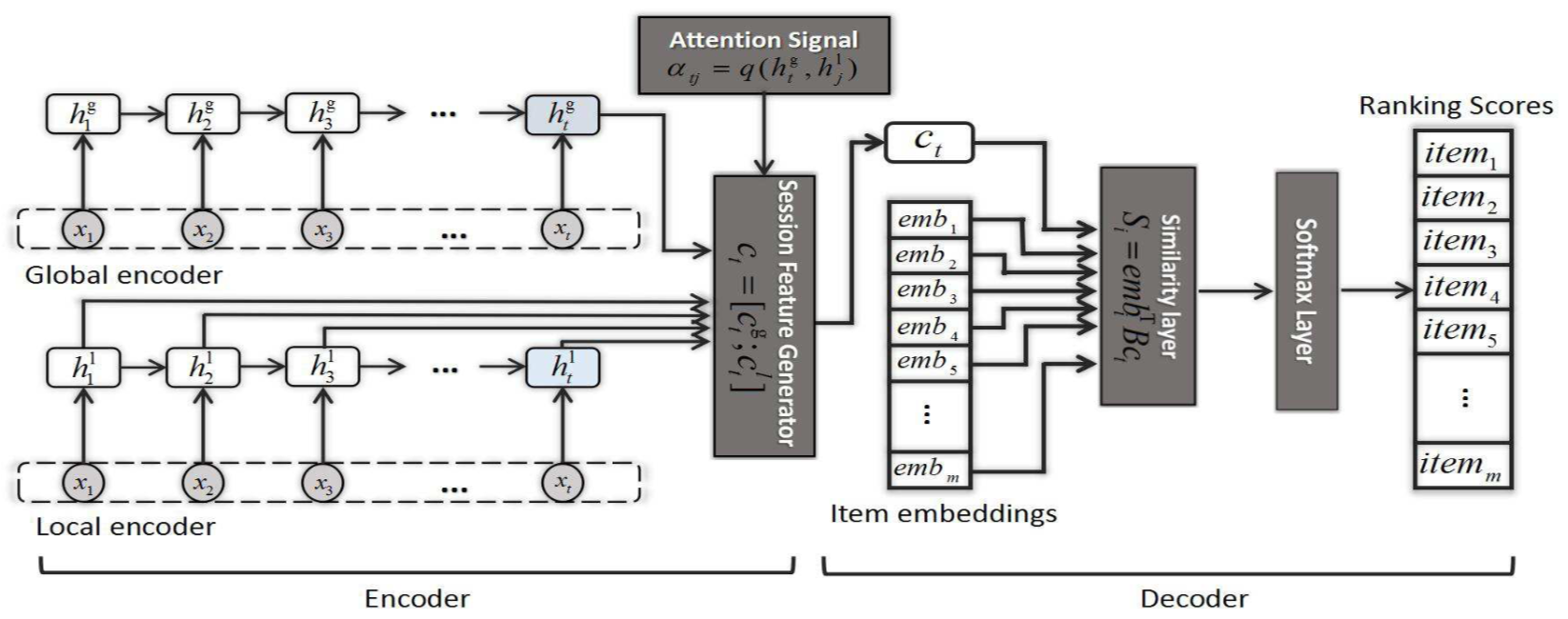
- 在Global序列信息的Encoder中,取了用户之前的所有行为(应该会卡一段阈值)来过了GRU之后取到的Final State作为Encoder的Embedding $c_t^g = h_t $
- 在Local中Session序列中的Encoder中,向全局信息的Encoder一样,只是最后输出之后取了一层Attention操作,希望突出当前序列中的一些重要行为。$$c_t^l = \sum_{j=1}^t \alpha_{i,j} h_j , \alpha_{i,j} = q(h_t,h_j)$$
- 然后最终Local和Global给Concat起来作为Encoder的输出$$c_t = [c_t^g;c_t^l]$$
- 接下来所有候选的Item按Embedding的方式来输入,称为$emb_i$
- 将Encoder的Embedding和候选集的Embedding进行
Bilinear操作:$$S_i=emb_i^T B c_t$$ - 这一步过后其实就会得到了各个候选项的一个score,进行softmax归一化之后可以作为各个候选项的概率$q_i$
- 最终的loss是$L(p,q) = -\sum_{i=1}^m p_i log(q_i)$
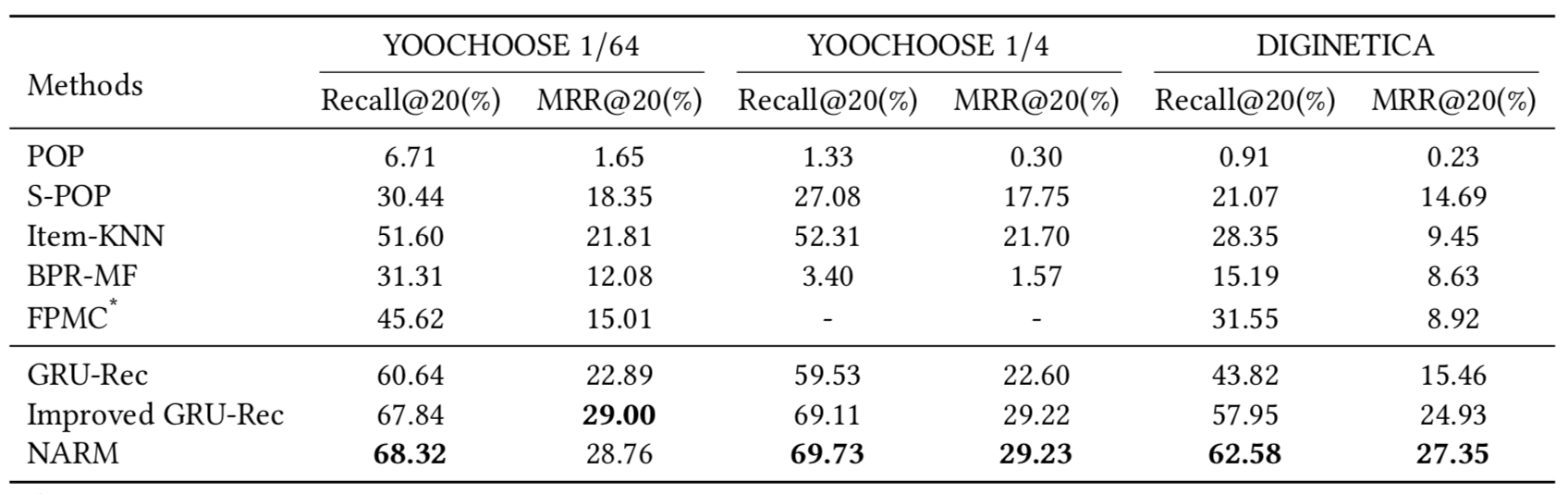
他的实验对比中,较于其他Baseline算法还是有不少的提升的,不过对于Improved GRU-Rec并没有太大优势
其实也可以理解,最大的贡献应该是在流推荐中同时考虑了Global和Local的结合,整个模型的思路还是很清晰简洁的,Encoder->Attention->Bilinear->Cross Entropy,但是也没有特别大的改进
特别是在Local中的Attention那一层,说的不明不白,他的$h_t$变量没有描述清楚,感觉就是一个非常普通的Self-Attention,也许在这一层的Attenion可以和Global中的信息结合起来。
RepeatNet
在购物场景中,因为有一些商品属性的原因,经常会去重复购买一些商品,比如纸巾-_-!!,因此用户其实存在着一些复购需求,类似这种场景的还有音乐、视频。
而实际的推荐系统中,我们经常在进行实时推荐时会根据用户历史记录直接去重,就算是缩短去重窗口也很少会刻意去推荐已经推荐过的item。RepeatNet非常机制的结合了类似copynet的idea,在模型的设计上给人一种眼前一亮的赶脚,他在进行推荐(Explore)中同时会有一定概率来推荐出历史行为(Repeat)。
该模型是在序列推荐的技术上加入了重推的概率进行Joint-Learning,以一种非常巧妙的方式来进行重推(类似point-generator的copy机制):
整个模型的优化目标是这样的:
$$P(i|I_s) = P(r|I_s) P(i|r,I_s) + P(e|I_s) P(i|e,I_s)$$
- 其中$I_s$表示用户的session行为记录
- 而$P(r|I_s)$表示需要进行重推的概率,这样$P(e|I_s)=1-P(r|I_s)$表示正常推荐的概率,
- $P(i|r,I_s)$则表示历史session中各个item被重推的概率,$P(i|e,I_s)$为候选item被推荐的概率了
因此整个RepeatNet其实是在做是否重推情况下各个候选item的联合概率最大化.
整个模型的结构是这样: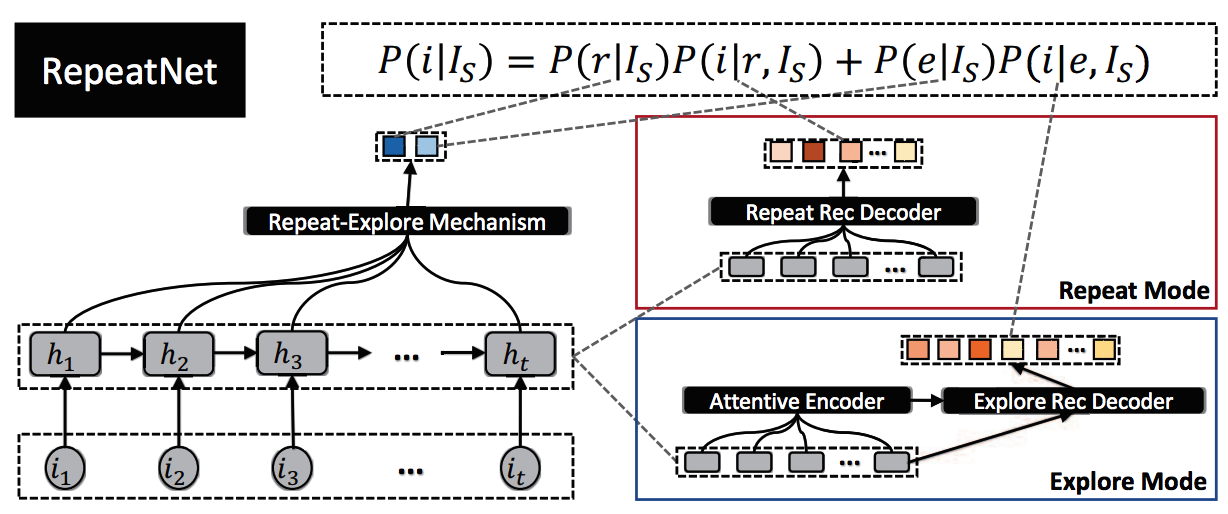
- 模型的输入一个一串序列:$I_s=i_1,i_2,i_3,…,i_t$
- 输入的序列$I_s$经过单向GRU之后得到每一步的状态$ST=[h_1,h_2,h_3,…,h_t]$
Repeat-Explore Mechanism:这里将$ST$过一个Self-Attention之后进行一个二分类,来计算Repeat和Explore的概率Repeat Model:这里需要走到重推的计算逻辑,重推是表示从$I_s$里面推荐出一个概率最高的,这里对于$I_s$序列的item对于每个$ST$都进行一次Attention的前置公式,直接使用Sofatmax的结果,可以理解为$\alpha$因子,具体的公式是这样的:
$$e^r_{\tau}=v^T_r tanh (W_rh_t+U_rh_{\tau}) \\
P(i|r,I_s)=\left\{
\begin{aligned}
\frac{exp(e^r_i)}{\sum_{\tau=1}^t exp(e^r_\tau)} & \quad i \in i_s \\
0 & \quad i \in I-I_s\\
\end{aligned}
\right.$$Explore Mode:在正常推荐时,会过一个Self Attention,然后时$h_t$进行concat,之后就是过一个正常的MLP层以及求softmax了
因此该模型在这里的损失函数有两个:
- 是否执行
Repeat还是Explore的损失函数:
$$L_{model} = -(\mathbb{I}(i \in I_s)\text{log}P(r|I_s) + (1-\mathbb{I}(i \in I_s))\text{log}P(e|I_s))$$ - 候选item概率分布的损失函数:
$$L_{rec} = \text{log}P(i_\tau|I_s)$$
最终该作者用了求和的方式来进行最终的优化:
$$L(\theta) = L_{model}+L_{rec} $$
在实验结果里面显示,该目前也取得了不少的提升: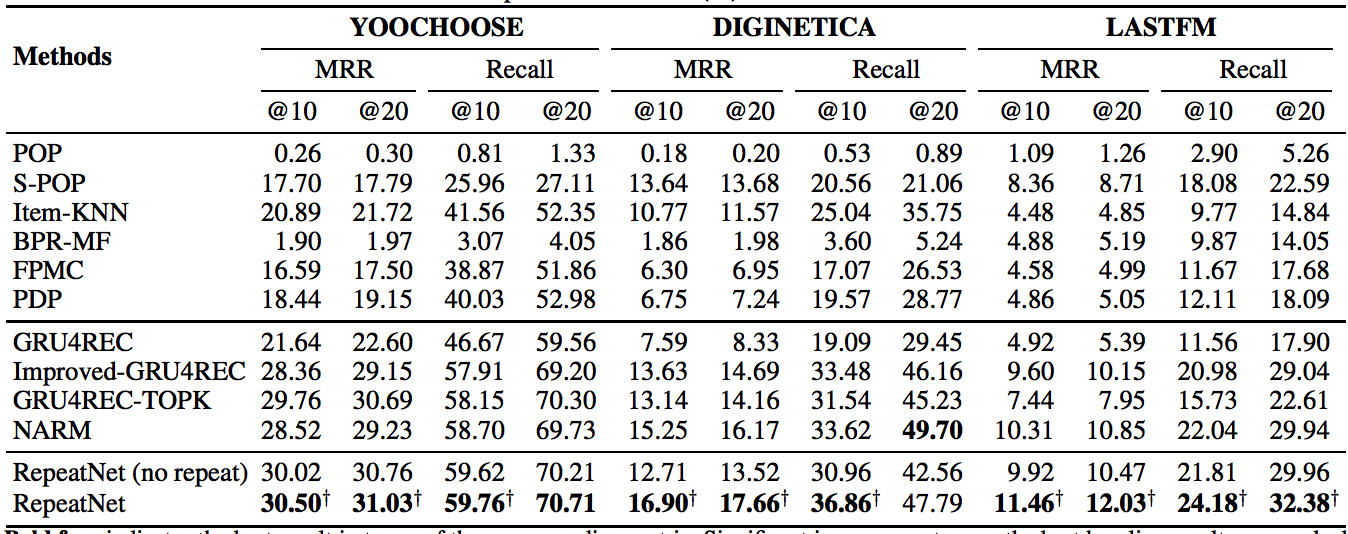
其实我到是可以理解为$RepeatNet$是一个更加贴合推荐实际的模型,结合了重推,但是其实在实际使用中可能还存在不少问题:
- 比如在最近topK个已经展现过的再重推是否合适,是否应该有一个阈值来控制。
- 另外还有一个其实短
Session内重复的量不会很高,那意味这个这个Train的Session会比较长,而在实际的场景中很少会用长session来做Inference,因为RNN-based的模型的预测速度和session长度成正比,并且Session太长也意味了效果会变差。
User-Based GRU
这个paper是在序列推荐模型的GRU模块里面加入用户信息,作者认为在序列建模时加入了用户特征之后能够更好的刻画整个行为序列,具体做法主要是针对GRU模块中加入User向量$v$进行倒腾,主要有三种集成的方式:
- Linear User Integration:线性方式的集成
- Rectified Linear User Integration:比线性更加柔和的一种方式
- Attentional User Integration: 以Attention的方式集成
Linear User Integration
针对给定GRU的Cell和用户向量下,这种集成是将用户向量加入到更gate的计算以及更新的state中,看下Cell图(其实这个图画的并不是很清晰-_-):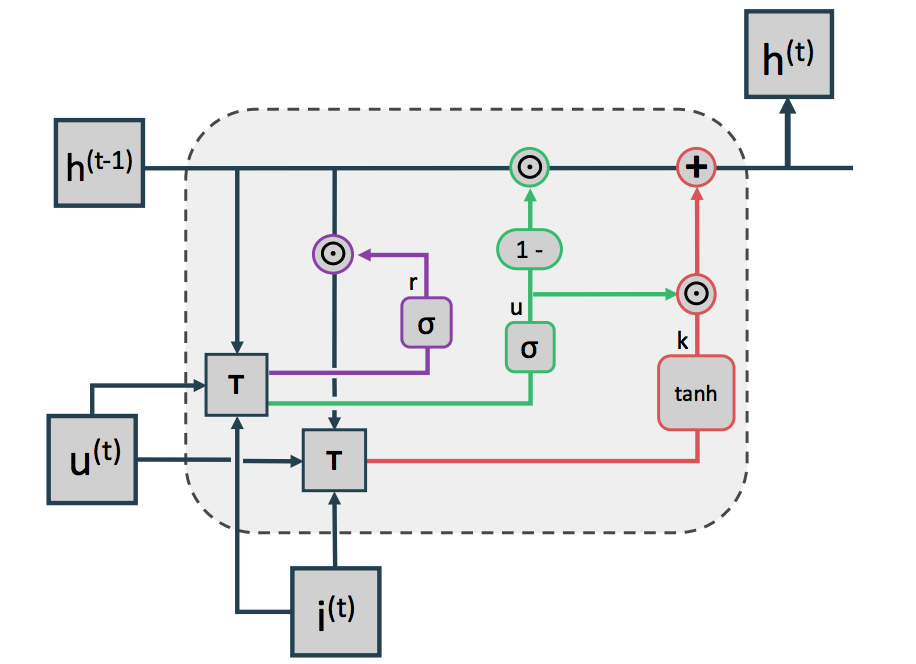
不过再配合一下公式就很清晰了:
$$\begin{bmatrix}
u \\
r
\end{bmatrix}
=
\begin{bmatrix}
\sigma \\
\sigma
\end{bmatrix}
T
\begin{bmatrix}
h^{t-1} \\
E_i^t \\
E_v^t
\end{bmatrix}$$
这是GRU两个门的输出,在计算门的时候加入了用户向量$E_v^t$,其余操作就是和正常的GRU一样了
Rectified Linear User Integration
但是针对线性的集成,可以发现用户向量在每一个step都是一样,并且是重复的,这样会增加整个训练的计算量,因此作者又想了一种更加柔和的方式来接入:
其实改图还是看不大清楚要表达的-_-
主要思想是 在每一个step时:
- 将输入向量和用户向量concat之后之后过两个MLP得到两个对比向量$\kappa_1 , \kappa_2$
- 当用户向量$E_v^t$的每个元素都小于$\kappa_1$时,将当前的step的用户向量直接置0(丢弃的意思)
- 当用户向量有部分小于$\kappa_2$时,对于用户向量的每个元素都乘以一个因子$\omega$
- 否则,正常使用当前step的用户向量
用公式来代替就是:
$$ E_v^t=\left\{
\begin{aligned}
0 & \quad \quad E_v^t< \kappa_1 \\
\omega \cdot E_v^t &\quad \quad \kappa_1 < E_v^t< \kappa_2 \\
E_v^t &\quad \quad \text{else} \\
\end{aligned}
\right.$$
然后其余步骤就是和线性的集成一样了
Attentional User Integration
先对普通线性集成的问题,作者又提了一个新的方式,他认为同一个用户向量在不同step下应该权重是不一样的,比如在t=0的时候,用户向量影响的作用应该是比较低(因为没有多少用户行为)
哈哈,其实我觉得要看用户向量怎么选了,如果该用户向量可以较为精准的表示用户向量了,这个时候t=0的时候用户的向量应该也是还蛮重要的。
因此不同的step下用户向量的权重应该是不同的,也就是类似Attention的方式了,但是其实感觉他paper里面和attention的思想还是有一些差异的,先看图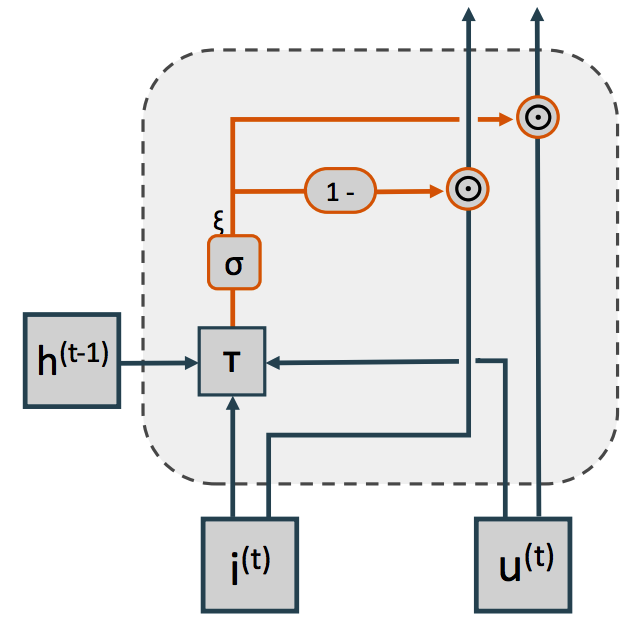
该集成方式会根据三个输入来计算一个门(gate:$\xi$)
$$ \xi = \sigma(T h^{t-1} + TE_i^t + TE_v^t)$$
这个$\xi$用来做每个step的输入向量和用户向量的一个平衡,因此GRU的门计算就是这样了:
$$\begin{bmatrix}
u \\
r
\end{bmatrix}
=
\begin{bmatrix}
\sigma \\
\sigma
\end{bmatrix}
T
\begin{bmatrix}
h^{t-1} \\
(1-\xi) E_i^t \\
\xi E_v^t
\end{bmatrix}$$
那再接下来的就是和线性集成一样了
所以后面两种集成的方式主要是针对线性集成每一步用同一个用户向量再改进的,他的实验效果是这样的: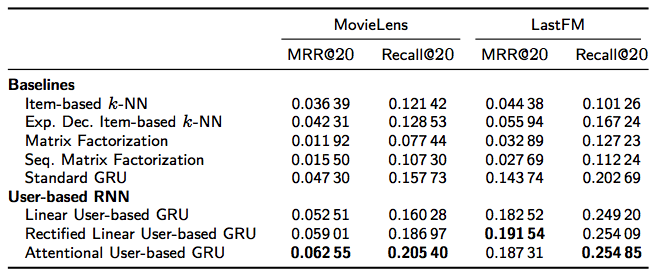
可以看到针对改进过的gru的效果还是有不少提升的.
其实在实际工业界里面有不少很成熟的算法框架中也会尝试将一些用户的全局信息/兴趣点通过gate机制来融入到gru中进行训练,能得到一些微弱提升,但是性价比而言相对比较低,当然有富余人员配置时还是值得尝试的。
SR-GNN
作者觉得用户的行为序列可以用图来表示,因此在传统的序列建模时改为使用$GNN^5$对来图进行建模,也就有了这个SR-GNN:
直接看架构图吧: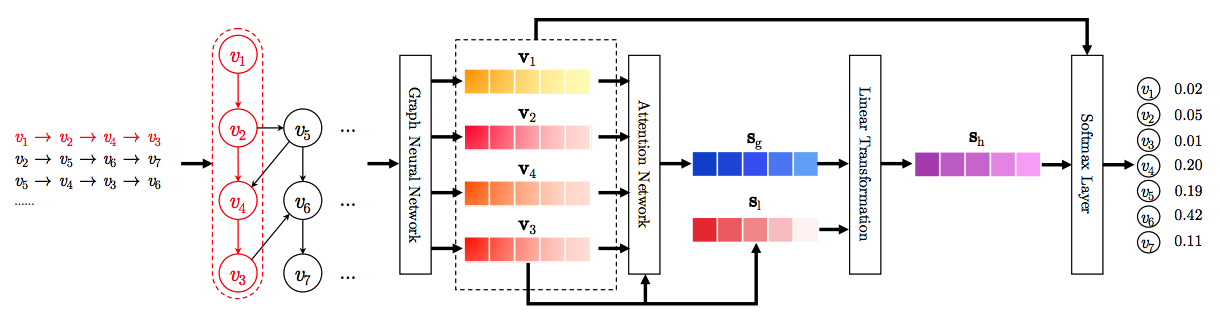
虽然图的头部画的session之间的item是有关联的,其实在model里面各个session其实是独立的-_-!!
最重要的是他的GNN那块,以$[v_1,v_2,v_3,v_2,v_4]$这个用户的session为例,可以将session用图表示为: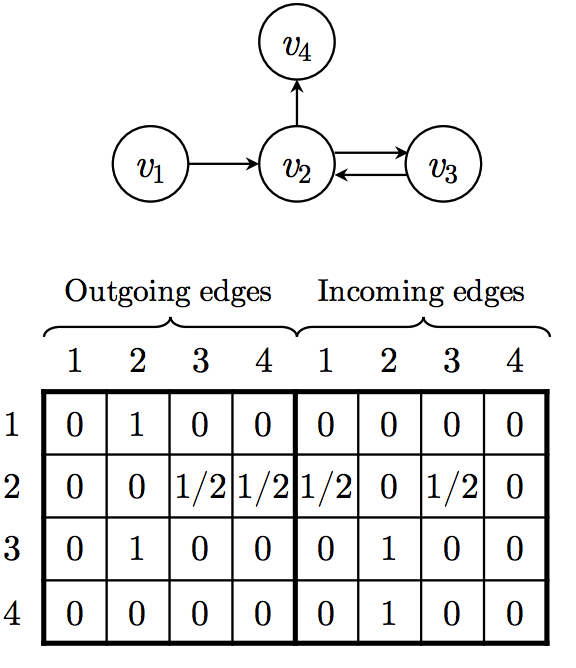
- 他使用邻接矩阵来表示
- 边之间的权重分为出度权重和入度权重
- 最终一个图可以用 一个带出度权重的矩阵和 带入度权重的矩阵来表示,他们的shape都是$[N,N]$
对于整个序列使用GNN来进行表达:
$$a_{s,i}^t = A_{s,i}^T [v_1^{t-1},…,v_n^{t-1}]^T H + b \\
z_{s,i}^t = \sigma(W_z a_{s,i}^t + U_z v_i^{t-1}) \\
r_{s,i}^t = \sigma(W_r a_{s,i}^t + U_r v_i^{t-1}) \\
\tilde{v_i^t} = \text{tanh}(Wa_{s,i}^t + U(r_{s,i}^t \odot v_i^{t-1} )) \\
v_i^t = (1-z_{s,i}^t) \odot v_i^{t-1} + z_{s,i}^t \odot \tilde{v_i^t}$$
其中
- $z$和$r$分布表示重置门和更新门,$\odot$ 表示
element-wise的相乘 - $A$矩阵其实就是session图的邻接矩阵,$a$向量用户表示相当step下图相关的向量,用于接下来模块的初始化
- 眼熟的一眼就看出来了,其实就是
GRU单元的公式,最大的差别就是初始化使用的是$a$,状态的维持使用的是$v$向量
额 其实就是
GATED GRAPH SEQUENCE NEURAL NETWORKS这篇中的式子
经过GNN之后可以得到每个节点的embdding,接下来将整个session用local和global两个节点别表示,其中:
local级别的embedding可以直接使用最后一个item的向量来表示,也就是$s_l = v_n$global级别的embedding使用$soft-attention$来表示$$a_i = q^T \sigma(W_1v_n + W_2v_i+c) \\ s_g = \sum_i^n \alpha_iv_i$$
最终的embedding是两个级别向量的合并转换:$$s_h = W_3[s_l;s_g]$$
其实可以看到最终的embedding里面其实是极大的加强的最后一个item的权重,之前做过相关实验,确实是最后一个item的embedding的最重要的
其训练时loss采用了经典的交叉熵。
实验效果再过一下: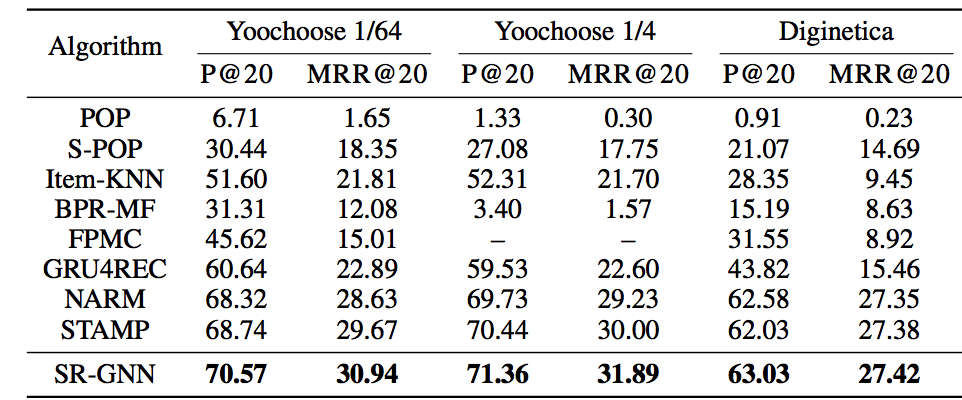
对比本文里面提到了NARM算法效果有提升,但是效果不是提升的很明显。
其实整个SR-GNN模型就是将序列模型是将GRU改成了GNN建模,感觉实用性并不是很高,因为单用户的常规单session中并没有太多可以形成图。-_-

